 |
Лекция 13. Основные выборочные характеристики |
1. Выборочная функция распределения |

 |
Лекция 13. Основные выборочные характеристики |
1. Выборочная функция распределения |

Замечание 1. Математическая статистика - это наука o математических методах, позволяющих по статистическим данным (реализациям СВ) построить теоретико-вероятностную модель исследуемого явления. Задачи математической статистики являются, в некотором смысле, обратными к задачам теории вероятностей. Центральным понятием математической статистики является выборка.
Определение 1. Случайной выборкой (выборкой) объема n называется случайный вектор
Zn | Δ = |
col(X1, ... , Xn), |
F(x) | Δ = FX. |
Замечание 2. В определении 1 выборка Zn рассматривается априорно (до опыта) и поэтому является случайным вектором. Если же рассматривать выборку апостериорно (после опыта), то она будет уже реализацией многомерной СВ Zn, т.е. неслучайным вектором
zn | Δ = |
col(x1, ... , xn) |
Пример 1. Пусть требуется определить неизвестную долю белых шаров в урне. По схеме случайного выбора с возвращением отобрано n шаров. Будем считать, что реализация xk СВ Xk равна 1, если k-ый выбранный шар оказался белым и xn = 0 в противном случае. Здесь СВ Xk независимы и одинаково распределены, причем вероятность p того, что будет извлечен белый шар
p | Δ = |
P{Xk = 1}, |
q | Δ = |
P{Xk = 0}, |
Zn | Δ = |
col(X1, ... , Xn) |
| ^ p |
Δ = |
1 n |
n ∑ k=1 |
Xk, |
Zn | Δ = |
col(X1, ... , Xn). |
zn | Δ = |
col(x1, ... , xn), |
p |
Δ = |
1 n |
n ∑ k=1 |
xk, |
| ^ p, |
Замечание 3. Одна из основных задач математической статистики состоит в вычислении статистических характеристик изучаемой СВ на основе информации, содержащейся в выборке.
Определение 2. Если апостериорную выборку x1, ... , xn располагать не в порядке ее получения (нижний индекс), а в порядке возрастания полученных значений (верхний индекс) x(1) ≤ x(2) ≤ ... ≤ x(n), то получим упорядоченный ряд апостериорной выборки. Если теперь обозначить через X(k), k = 1,n, случайные величины, которые при каждой реализации zn априорной выборки Zn принимают k-ые (по верхнему номеру) значения x(k), то получим упорядоченную последовательность СВ X(1) ≤ ... ≤ X(n), называемую вариационным рядом выборки.
Определение 3. Элементы X(k) вариационного ряда называются порядковыми статистиками, а крайние члены вариационного ряда X(1), X(n) - экстремальными порядковыми статистиками.
Определение 4. Пусть x - произвольная точка на оси Ox, а M(x) - случайное число элементов априорной выборки объема n, попавших не правее точки x. Таким образом, если x(1) ≤ ... ≤ x(i-1) ≤ x ≤ x(i) ≤ ... ≤ x(n), то реализация СВ M(x) равна m(x) = i-1, где m(x) - конкретное число элементов из реализации x(1), ... , x(n) вариационного ряда, попавших левее точки x. Частота
| ^ Fn |
Δ = |
M(x)/n |
Fn |
Δ = |
m(x)/n |
| ^ Fn(x) |
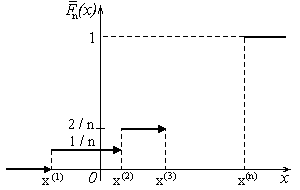
Рисунок 1.
Замечание 4. Выборочная функция распределения
| ^ Fn(x) |
| ^ Fn(x) |
p | Δ = |
P{Xk ≤ x} | Δ = |
F(x), q | Δ = |
P{Xk > x} = 1 - F(x). |
| ^ Fn |
Δ = |
M(x)/n |
^ Fn |
п.н. → |
F(x). |
2. Гистограмма |

Замечание 1. Рассмотрим процедуру группировки выборки. Для этого разделим точками α0, ... , αj+1 действительную ось R1 = (-∞,+∞) на
L |
Δ = |
j+1 |
pk |
Δ = |
mk / n, |
Определение 1. Последовательность детерминированных величин pk, k = 1, j-1 , называется статистическим рядом, а его реализация представляется в виде таблицы:
| (α1,α2] | ... | (αj-1,αj] |
| p1 | ... | pj-1 |
Определение 2. Изобразим графически статистический ряд. На оси Ox отложим разряды и на них, как на основании, построим прямоугольники, имеющие площадь pk. Полученная ступенчатая функция fn называется гистограммой рис.2.
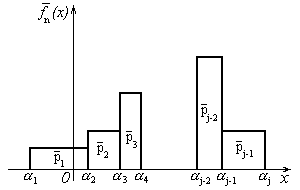
Рисунок 2.
Замечание 2. На интервалах (-∞,α1] и [αj,+∞) построить такие прямоугольники нельзя, так как α1 < x(1), αj < x(n). Необходимость введения разрядов Δ0 и Δj будет ясна из лекции 16.
3. Выборочные среднее и дисперсия |

Определение 1. Для выборки объема n выборочными начальными и центральными моментами порядка r (r = 1,2,...) называются соответственно СВ
| ^ νr | Δ = |
1 n |
n ∑ k=1 |
(Xk)r , |
^ μr |
Δ = |
1 n |
n ∑ k=1 |
(Xk- |
^ ν1 |
)r . |
Определение 2. Выборочным средним и выборочной дисперсией называются соответственно
| ^ MX | Δ = |
^ ν1 | Δ = |
1 n |
n ∑ k=1 |
Xk , |
^ DX |
Δ = |
^ μ2 |
Δ = |
1 n |
n ∑ k=1 |
(Xk- |
^ MX |
)2 . |
Замечание 1. При достаточно общих предположениях о виде неизвестной функции распределения F(x) выборочные моменты близки к соответствующим теоретическим характеристикам νr, μr.
|
^ ^ |

1)
M[ |
^ MX |
] = mX , |
mX | Δ = |
M[X]. |
M[ |
^ MX] | Δ = |
M[ |
1 n |
n ∑ k=1 |
Xk] |
2)mx = |
1 n |
M[ |
n ∑ k=1 |
Xk] = mX . |
2)
D[ |
^ MX |
] = dX / n , |
dX | Δ = |
D[X]. |
D[ |
^ MX] | Δ = |
D[ |
1 n |
n ∑ k=1 |
Xk] |
7)mx = |
1 n2 |
D[ |
n ∑ k=1 |
Xk] |
4)M[X] = |
1 n2 |
n ∑ k=1 |
D[Xk] = |
dX n |
. |
3)
M[ |
^ DX] = |
n-1 n |
DX . |
M[ |
^ DX] | Δ = |
M[ |
1 n |
n ∑ k=1 |
(Xk - |
^ MX |
)2] |
Δ = |
1 n |
M[ |
n ∑ k=1 |
(Xk - |
1 n |
n ∑ i=1 |
Xi)2] |
1)M[X] = |
| = | 1 n |
n ∑ k=1 |
M[(Xk - | 1 n |
n ∑ i=1 |
Xi)2] = | 1 n |
n ∑ k=1 |
M[(Xk - mX - | 1 n |
n ∑ i=1 |
(Xi - mX))2]= |
= |
1 n |
n ∑ k=1 |
M[( |
n-1 n |
(Xk - mX) - |
1 n |
∑ i≠k |
(Xi - mX))2] |
4)M[X] = |
| = | 1 n |
n ∑ k=1 |
( | (n-1)2 n2 |
dX + | n-1 n2 |
dX) = | n-1 n |
dX . |
Замечание 2. Таким образом, МО выборочного среднего совпадает с МО СВ X, а МО выборочной дисперсии
| ^ DX |
| ^ DX |
| ^ DX |
| ^ SX | Δ = |
n n-1 |
^ DX . |
Определение 3. Несмещенной выборочной дисперсией называется СВ:
| ^ SX | Δ = |
1 n-1 |
n ∑ k=1 |
(Xk- |
^ MX |
)2 = |
n n-1 |
^ DX . |
4)
M[ |
^ SX |
] = dX . |
M[ |
^ SX |
] = |
n n-1 |
M[ |
^ DX |
] |
^ 3)M[X] = |
dX . |
