Лекция 4. Основные понятия |
1. Функция распределения |

Лекция 4. Основные понятия |
1. Функция распределения |

Определение 1. Случайной величиной (СВ) X называется такая функция X(ω)
элементарного события ω с областью определения Ω и областью значений R1, что событие {ω : X(ω) ≤ x} принадлежит σ-алгебре Б при любом действительном x О R1. Значения x функции X(ω) называются реализациями СВ X(ω).Замечание 1. Случайные величины будем обозначать прописными (большими) латинскими буквами X, Y, Z, а их возможные значения (реализации) - соответствующими строчными (малыми) буквами x, y, z.
Определение 2. Совокупность всех
реализаций СВ, т.е. область значений функции X(ω), называется спектром значений СВ.Определение 3.
Спектр значений СВ называется дискретным, если он состоит из конечного или счётного числа элементов (т.е. можно установить взаимно однозначное соответствие между всеми его элементами и некоторым подмножеством положительных целых чисел).Определение 4. Спектр значений
СВ называется непрерывным, если он является связным множеством (т.е. каждый отрезок, соединяющий два произвольных элемента спектра, содержится в этом множестве).Пример 1. Пусть
опыт G состоит в бросании двух монет, а элементарным событием ω является положение упавших монет. Тогда число выпавших "гербов" есть СВ X(ω) с конечным числом возможных значений {0,1,2}, т.е. с дискретным спектром, а расстояние между центрами упавших монет есть СВ Y(ω) с непрерывным спектром, который является полуосью 0 ≤ y < ∞.Определение 5. Законом распределения СВ называется любое правило (таблица, функция), позволяющее находить
вероятности всех возможных событий, связанных с СВ.Определение 6. Рассмотрим
вероятность P{ω : X(ω) ≤ x} события {ω : X(ω) ≤ x} для различных x О R1. Вероятность| Fx(x) | Δ = |
P{ω : X(ω) ≤ x}, |
Замечание 2. Данная вероятность
Fx(x) определена, поскольку рассматриваемые события принадлежат классу Б (определение Л1.Р3.О4). Далее для простоты записи мы будем обозначать| X | Δ = |
X(ω), {X ≤ x} | Δ = |
{ω : X(ω) ≤ x}, F(x) | Δ = |
Fx(x) | Δ = |
P{ X ≤ x}. |
Замечание 3.
Функция распределения является разновидностью закона распределения для СВ всех типов и однозначно определяет СВ. Далее вместо фразы "СВ, имеющая функцию распределения F(x)" будем говорить для краткости: "СВ с распределением F(x)".
1)
F(x) определена для всех x О R1 по определению 6.2) 0 ≤
F(x) ≤ 1 для всех x О R1. Так как F(x) - вероятность, то данное свойство следует из свойства 5)P и аксиомы А1.3)
F(-∞) = 0, F(∞) = 1. Пусть| Bn | Δ = |
{ X ≤ -n}, |
| {X ≤ -∞} = | ∞ ∏ n=1 |
Bn = Ж , |
| F(-∞) = | l i m n→∞ |
P(Bn) = 0. |
| An | Δ = |
{ X ≤ n} и Bn | Δ = |
Ω \ An, |
| F(+∞) = | l i m n→∞ |
P(An) = 1 - |
l i m n→∞ |
P(Bn) = 1. |
4)
F(x2) - F(x1) = P{x1 < X ≤ x2}, если x2 > x1. Посколькуто по аксиоме А3:
| F(x2) | Δ = |
P{X ≤ x2} = F(x1) + P{x1 < X ≤ x2}. |
5)
F(x2) ≥ F(x1) для x2 > x1, т.е. F(x) не убывает. Это следует из свойства 4)F(x):6)
| F(x) = |
l i m ε → 0 |
F(x + ε), при ε > 0, |
 |
2. Дискретные случайные величины |

Определение 1.
СВ называется дискретной, если её спектр значений является дискретным.Определение 2. Простейшей формой
закона распределения дискретной СВ является ряд распределения| pk | Δ = |
P{X = xk}, k = 0,n , |
| X | x0 | . . . | xn |
| P | p0 | . . . | pn |
Замечание 1. p0 + ... + pn = 1, так как
события {X = x0}, ... , {X = xn} несовместны и образуют полную группу.Определение 3. Графическое изображение
ряда распределения называют многоугольником распределения (рис. 1).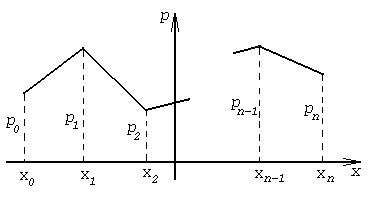
Рисунок 1.
Замечание 2.
Распределение вероятностей аналогично понятию "распределение единичной массы вдоль бесконечного стержня Ox" используемому в механике (этим, в частности, можно объяснить использование в теории вероятностей термина "распределение"). Для дискретного распределения возможна следующая механическая интерпретация: на оси Ox распределена единичная масса так, что массы p0, ... , pn сосредоточены в отдельных точках x0, ... , xn.Определение 4. Единичной ступенчатой функцией или функцией Хевисайда называется функция вида (см. рис. 2)
| l(x) | Δ = |
{ | 0, x < 0, 1, x ≥ 0. |
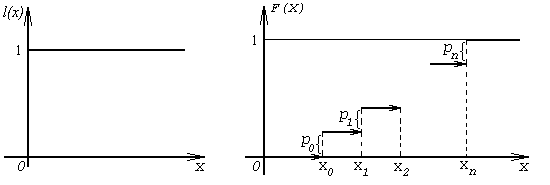
Рисунок 2 Рисунок 3.
Замечание 3. Для
дискретной СВ, используя ряд распределения и l(x), можно построить функцию распределенияF(x) = p0l(x-x0) + ... + pnl(x-xn).
Функция распределения дискретной СВ является ступенчатой(см. рис. 3), причем в точках разрыва F(x) величины скачков равны вероятностям p0, ... , pn соответствующих реализаций x0, ... , xn СВ X.
 |
3. Непрерывные случайные величины |

Определение 1. СВ X с непрерывной
функцией распределения Fx(x) называется непрерывной.Определение 2. Плотностью распределения (плотностью вероятности)
СВ X называется неотрицательная кусочно-непрерывная функция fX(x), для которой при любом x О R1 выполняется соотношение| Fx(x) = | x ∫ -∞ |
fx(t) dt . |
Замечание 1. Для простоты дальнейших обозначений будем писать
| f(x) | Δ = |
fx(x). |
Определение 3. СВ, у которой существует
плотность вероятности, называется абсолютно непрерывной.Замечание 2. Из
определения 2, используя правило дифференцирования интеграла с переменным верхним пределом, получаем, что в точках непрерывности плотности f(x) производная функции распределения совпадает с плотностью, т.е. F'(x) = f(x).Замечание 3. Кроме
абсолютно непрерывных СВ имеются непрерывные СВ, называемые сингулярными, которые не имеют плотности вероятности. В дальнейшем такие СВ не рассматриваются, а под непрерывными СВ понимаются абсолютно непрерывные СВ.Замечание 4.
Плотность вероятности является разновидностью закона распределения для непрерывных СВ.Замечание 5. Используя свойство
4)F(x) и замечание 2, рассмотрим пределl i m Δx→0 |
P{x ≤ X ≤
x + Δx} Δx |
= | l i m Δx→0 |
F(x + Δx) -
F(x) Δx |
Δ = |
F'(x) = f(x). |

1)
f(x) ≥ 0 для всех x О R1 , т.е. выполняется условие неотрицательности плотности. Это свойству следует из определения 2.2)
| +∞ ∫ -∞ |
f(x) dx = 1 , |
| F(x) = | x ∫ -∞ |
f(x) dx , |
| +∞ ∫ -∞ |
f(x) dx = F(∞) = 1. |
3)
| x2 ∫ x1 |
f(x) dx = P{x1 ≤ X ≤ x2}. |
| x2 ∫ x1 |
f(x) dx = | x2 ∫ -∞ |
f(x) dx - | x1 ∫ -∞ |
f(x) dx = F(x2) - F(x1) = |
4) Рассмотрим
СВ| Y | Δ = |
φ(x), |
| ψ(y) | Δ = |
φ-1(y), |
FY(y) |
Δ = |
P{φ(X) ≤ y} = |
| |
φ(x) и ψ(y) - строго возрастающие |
| |
= |
| = P{X ≤ ψ(y)) = | ψ(y) ∫ -∞ |
fx(x) dx = |
| = | | | замена переменной x на y , x = ψ(y) |
| | = | y ∫ -∞ |
fx(ψ(y))ψ'(y) dy . |
| fY(y) = F'Y(y) = | d dy |
( | y ∫ -∞ |
fx(ψ(y))ψ'(y) dy) = fx(ψ(y))ψ'(y). |
FY(y) |
Δ = |
P{φ(X) ≤ y} = P{X ≥ ψ(y)) = |
+∞ ∫ ψ(y) |
fx(x) dx = |
| = | +∞ ∫ y |
fx(ψ(y))ψ'(y) dy = 1 - | y ∫ -∞ |
fx(ψ(y))ψ'(y) dy ; |
| fY(y) = | d dy |
(1 - | y ∫ -∞ |
fx(ψ(y))ψ'(y) dy) = - fx(ψ(y))ψ'(y). |
Пример 1. Рассмотрим СВ
| Y | Δ = |
aX + b, |
| fY(y) = | 1 |a| |
fx | ( | y-a a |
) | . |
 |
4. Числовые характеристики случайных величин |

Определение 1. Детерминированная величина
mx |
Δ = |
M[X] = |
+∞ ∫ -∞ |
xf(x) dx |
Замечание 1. В механике число
+∞ ∫ -∞ |
xf(x) dx |
Замечание 2. Для
дискретной СВ X с конечным числом значений под математическим ожиданием понимается величинаmx |
Δ = |
M[X] |
Δ = |
n ∑ k=0 |
pkxk , где pk |
Δ = | P{X = xk}. |
Замечание 3. Для СВ
Y |
Δ = |
φ(X) |
M[φ(X)] = |
+∞ ∫ -∞ |
φ(x)f(x) dx, |
Определение 2. Начальными νr и центральными μr моментами порядка r (r = 1, 2, ...)
непрерывной СВ X называются детерминированные величиныνr |
Δ = |
M[Xr] |
Δ = |
+∞ ∫ -∞ |
xrf(x) dx ; μr |
Δ = | M[(X-mx)r] |
Δ = |
| Δ = |
+∞ ∫ -∞ |
(x-mx)rf(x) dx . |
Замечание 4. Для
дискретной СВ с конечным числом значений интегралы в определении 2 заменяются суммами:νr |
Δ = |
n ∑ k=0 |
xkrpk , μr |
Δ = |
n ∑ k=0 |
(xk-mx)rpk. |
Определение 3.
Центральный момент второго порядка μ2 называется дисперсией СВ X и обозначаетсяdx |
Δ = |
D[X] |
Δ = |
μ2. |
Замечание 5.
Дисперсия dx характеризует степень рассеивания реализаций СВ X около ее МО.Определение 4. Средним квадратическим отклонением (СКО) СВ X называют величину
σx |
Δ = |
√dx ≥ 0. |
Определение 5. СВ
o X |
Δ = |
X - mx |
* X |
Δ = |
o X / σx |

1)
M[C] = C, если C - константа. Действительно, пусть X - дискретная СВ, принимающая значение C с вероятностью 1, т.е. P{X = C} = 1.ТогдаM[X] |
Δ = |
CP{X = C} = C. |
2)
M[CX] = CM[X], если C - константа, так какM[CX] |
Δ = |
+∞ ∫ -∞ | Cxf(x) dx = C |
+∞ ∫ -∞ | xf(x) dx |
Δ = | Cmx. |
3) M[X + C] =
mx + C, если C - константа, так какM[X + С] |
Δ = |
+∞ ∫ -∞ | (x + C)f(x) dx = |
+∞ ∫ -∞ | xf(x) dx + |
+∞ ∫ -∞ |
Cf(x) dx = mx + C. |
4) |
M[X]| ≤ M[|X|], поскольку|M[X]| |
Δ = |
| | +∞ ∫ -∞ | xf(x) dx |
| | ≤ |
+∞ ∫ -∞ | |x|f(x) dx |
Л4.Р4.33 = | M[|X|]. |
5)
M[ |
* X |
] = 0, D[ |
* X | ] = 1. |
M[ |
* X |
] |
Δ = |
M | [ |
X-mx σx |
] | , |
M[ |
* X | ] = 0, |
D[ |
* X | ] |
Δ = |
M[( |
* X |
-M[ |
* X |
])2] = |
1 σx2 |
M[(X-mx)2] = |
D[X] σx2 |
= 1. |
6)
D[X] = M[X2] - mx2. Действительно,D[X] |
Δ = |
M[(X-mx)2] |
Л4.Р4.33 = |
+∞ ∫ -∞ |
(x-mx)2f(x) dx = |
= |
+∞ ∫ -∞ |
(x2-2xmx+mx2)f(x) dx = M[X2] - 2M[X]mx + mx2 = M[X2] - mx2. |
7)
D[CX]=C2D[X], D[C+X] = D[X], где C - константа.8) Если D[X] = 0, то X = const с вероятностью 1. Действительно, если бы, например, СВ X принимала два значения x0 ≠ x1 с вероятностями p0 и p1 соответственно, то mX ≠ x0 и mX ≠ x1, т.к. mX = p0x0 + p1x1. Поэтому по замечанию
4 в этом случае было бы D[x] >0.Замечание 6. Свойства
2)mX-6)mX, доказанные выше для непрерывных СВ, справедливы также и для дискретных СВ. |
5. Характеристическая функция |

Определение 1. Характеристической функцией называется комплекснозначная функция
gx(t) |
Δ = |
M[eitX] |
Л4.Р4.З3 = |
+∞ ∫ -∞ |
eitxfx(x) dx , |
где t О R1 i2 = -1 , eitx |
Δ = |
cos tx + i sin tx. |
Замечание 1.
Характеристическая функция представляет собой преобразование Фурье плотности вероятности fx(x) СВ X. Поэтому обратное преобразование Фурье приводит к соотношениюfx(x) = |
1 2π |
+∞ ∫ -∞ |
e-itxgx(t) dt . |
g(t) |
Δ = |
gx(t), |
Замечание 2. Для
дискретной СВ X с конечным числом значений имеемg(t) |
Δ = |
n ∑ k=0 |
pkeitxk . |

1) |
g(t)| ≤ 1 для всех t О R1 . Так какeitx |
Δ = |
cos tx + i sit tx, то |eitx|2 = cos2 tx + sin2 tx = 1, |
|g(t)| ≤ |
+∞ ∫ -∞ |
|eitx|f(x) dx = 1. |
2)
g(0) = 1, поскольку eit0 = 1 иg(0) = |
+∞ ∫ -∞ |
f(x) dx = 1. |
3) Продифференцируем r раз функцию g(t):
dr dtr |
g(t) |
Δ = |
dr dtr |
(M[eitX]) = M |
[ |
dr dtr |
eitX |
] |
= irM[XreitX]. |
νr |
Δ = |
M[Xr] = |
1 ir |
dr dtr |
g(t) |
| | t =0 | . |
4) Пусть Y = aX + b, где X -
СВ с плотностью fx(x) и характеристической функцией gx(t). ТогдаgY(t) |
Δ = |
M[eit(aX+b)] = eitbM[eitaX] = eitbgX(at). |
 |
6. Квантиль |

Определение 1. Квантилью уровня p
функции распределения F(x) СВ X называется минимальное значение xp , при котором функция распределения F(x) не меньше значения p (см. рис. 4), т.е.xp |
Δ = |
min{ x : F(x) ≥ p}, p О (0,1). |
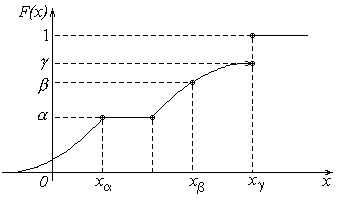
Рисунок 4.
Замечание 1. Если
функция распределения строго монотонна и непрерывна, то квантиль является единственным решением уравнения F(xp) = p.Определение 2.
Квантиль уровня p = 1/2 называется медианой.Замечание 2. Если
плотность распределения существует, строго положительна и симметрична относительно нуля, то xp = -x1-p. Действительно, пусть СВY |
Δ = |
-X. |
+∞ ∫ x1-p |
fx(x) dx = p, |
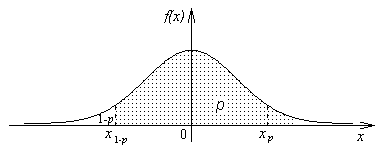
Рисунок 5.
Замечание 3.
Квантиль, наряду с уровнем значимости p является одной из основных статистических характеристик, используемых в математической статистике (см. часть 5).