Лекция 2. Основные свойства вероятности |
1. Аксиоматические свойства |

Лекция 2. Основные свойства вероятности |
1. Аксиоматические свойства |

Определение 1. Если
P(A) = 1, но A не равно Ω, то говорят, что событие A в опыте G происходит почти наверное (п.н.).Определение 2. Если
P(A) = 0, то говорят, что событие A почти никогда не происходит в опыте G.
1) Пусть
P(A) = 1. По аксиоме A2: P(Ω) = 1, но из этого не следует, что A = Ω (т.е. что A является достоверным событием).2)
P(Ж) = 0, т.е. вероятность невозможного события равна нулю. Во-первых, Ж О Б , поскольку σ-алгебре Б принадлежит само событие Ω и его дополнениеΩ |
Δ = |
Ω \ Ω = Ж. |
P(Ω+Ж) = P(Ω) |
A2 = |
1 , |
P(Ω+Ж) = |
| |
Ω • Ж = Ж, т.к. события Ω и Ж несовместны |
| |
A3 = |
P(Ω) + P(Ж) |
A2 = |
1 + P(Ж). |
3) Пусть
P(A) = 0. По свойству 2)P имеем P(Ж) = 0, но из этого не следует, что A = Ж, т.е. событие A не обязательно является невозможным.4) Если A
М B, то P(A) ≤ P(B), т.е. вероятность монотонна. Представим множество B как B = A+B \A (см. рис. 1).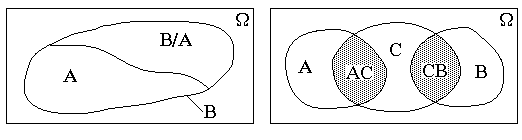
Рисунок 1 Рисунок 2.
По построению, A(B\A) =
Ж, следовательно, события A и B\A несовместны. Поэтому по аксиомам А3 и А1 имеем P(B) = P(A) + P(B\A) ≥ P(A).5)
P(A) ≤ 1 для любого A М Б . Так как A М Ω, то из свойства 4)P следуетP(A) ≤ P(Ω) |
A2 = |
1 . |
6)
P(A+B) = P(A) + P(B) - P(AB) для любых A, B О Б. Представим A в виде A = A\B + AB. Очевидно, (A\B)(AB) = Ж. Тогда по аксиоме А3: P(A) = P(A\B) + P(AB), откудаАналогичным образом поступим с событием A+B. Имеем A+B = B+A\B, причём B(A\B) = Ж. Тогда из аксиомы А3 следует
Подставляя в данное выражение формулу для P(A\B), получаем требуемое выражение.
7) P(A
+B) ≤ P(A) + P(B). Из аксиомы А1 следует, что P(AB) ≥ 0, поэтому по свойству 6)P получаемP(A+B) = P(A) + P(B) - P(AB) ≤ P(A) + P(B).
Замечание 1. Используя
свойство 7)P, по индукции можно получить неравенство| P( |
n ∑ i=1 |
Ai) ≤ | n ∑ i=1 |
P(Ai) , |
| P( | n ∑ i=1 |
Ai) = | n ∑ i=1 |
P(Ai) , |
8) Пусть события A и B несовместны, т.е. AB = Ж. Тогда верно
P(C(A+B)) = P(CA) + P(CB). По предположению имеем (CA)(CB) = Ж, так как AB = Ж. И, кроме того, по свойству событий 10)А имеем C(A+B) = CA + CB. Следовательно, по аксиоме А3 получаем (см. рис. 2)
P(C(A+B)) = P(CA + CB) = P(CA) + P(CB).
 |
2. Свойства вероятности для полной группы событий |

Определение 1. События H1, ..., Hn в
опыте G образуют полную группу несовместных событий, если они попарно несовместны (HiHj = Ж при i ≠ j) и в результате опыта произойдёт хотя бы одно из событий Hi, i = 1,n, т.е. H1+ ... + Hn = Ω. При этом события H1, ..., Hn, имеющие положительные вероятности, называются гипотезами.
9) Если
события H1, ..., Hn образуют полную группу, тоДанное свойство непосредственно вытекает из определения 1 и аксиом А3 и А2.
10) P(A) = 1 - P(A). По определению A =
Ω\A, поэтому AA = Ж. По свойству 12)А: A + A = Ω, т.е. события A и A образуют полную группу. Следовательно, по свойству 9)P: P(A+A) = 1. Так как A и A несовместны, то по аксиоме А3 имеем: 1 = P(A+A) = P(A) + P(A), откуда следует искомая формула.Пример 1. Пусть выстрел по цели производится случайным образом, а
события A и A соответствуют попаданию и промаху. Если известна вероятность попадания P(A) = p, где 0 ≤ p ≤ 1 , то вероятность промаха, т.е. события A, можно найти по свойству 10) P:q |
Δ = |
P(A) = 1 - P(A) = 1 - p. |
11)
P(A+B) = 1 - P(A•B). По свойству 11)A имеем A+B = A•B. Поэтому из свойства 10)P следует P(A+B) = 1- P(A+B) = 1 - P(A•B).12)
P(AB) = 1 - P(A+B). Это следует из свойства 11)P, если вместо событий A и B рассматреть соответственно события A и B и использовать свойство событий 12)A:| = A = A. |
13) Если
опыт G сводится к схеме случаев, то P(ωi) = p = 1/n, i = 1,n. Действительно, так как события ω1, ..., ωn несовместны, то1 |
A2 = |
P(Ω) = P(ω1 + ... + ωn) |
А3 = |
P(ω1) + ... + P(ωn) = np. |
Определение 3. Рассмотрим в
опыте G, сводящимся к схеме случаев, произвольное событие A, которое можно представить в виде суммы m случаев , т.е.| A = ωi | 1 | + ... + ωi | m | , |
| ωi | 1 | , ... , ωi | m |
14) Если
событие представимо в виде суммы m благоприятствующих случаев из общего числа n случаев, то вероятность такого события находится по классической формуле вычисления вероятности P(A) = m / n. Действительно,| P(A) = P(ωi | 1 | + ... + ωi | m | ) = P(ωi | 1 | ) + ... + P(ωi | m | ) = m / n. |
Пример 2. Опыт состоит в бросании игральной кости. Требуется найти вероятность выпадения четной грани (события A). В данном случае опыт сводится к
схеме случаев, в качестве которых можно взять все элементарные события ωi, i = 1,n. Тогда n = 6, а m = 3, поскольку A = ω2+ ω4+ ω6. Таким образом, P(A) = 1/2.Определение 4. Условной вероятностью P(A|B) события A относительно события B, если P(B) > 0, называется вероятность осуществления события A при условии, что событие B уже произошло и это известно. Условная вероятность по определению равна
P(A|B) |
Δ = |
P(AB) / P(B). |
15) Рассмотрим
опыт G, сводящийся к схеме случаев, и предположим, что событиям A, B, AB благоприятствуют соответственно mA, mB > 0, mAB случаев из всех n возможных. Допустим, событие B уже произошло. Это означает, что из всех возможных n случаев реально могло появиться только mB случаев, причём из них только mAB случаев благоприятствуют событию A. Тогда P(A|B) = mAB / mB. Действительно получаем:| P(A|B) | Δ = |
P(AB) P(B). |
14)P = |
mAB n
n mB |
= | mAB mB |
16) P(AB) = P(A)P(B|A) = P(B)P(A|B). Данная формула следует из определения 4 и свойства 9)А коммутативности операции умножения событий: AB = BA. Действительно,
17) P(A|Ω)=P(A). Это проверяется непосредственно:
P(A|Ω) |
= |
P(AΩ) P(Ω) |
2)А = |
P(A) P(Ω) |
А2 = P(A). |
