Лекция 10. Закон больших чисел |
1. Виды сходимости последовательностей случайных величин |

Лекция 10. Закон больших чисел |
1. Виды сходимости последовательностей случайных величин |

Замечание 1. В замечании Л1.Р3.З1. при определении вероятности по Мизесу указывался эмпирический факт, состоящий в устойчивости частоты появления события A в исследуемом опыте G при последовательном его повторении. Этот экспериментальный факт может быть обоснован математически с помощью закона больших чисел. Но для этого нам понадобятся некоторые понятия, характеризующие сходимость последовательности СВ.
Определение 1. Бесконечная последовательность СВ Xn, n = 1,2, ..., определенная на одном пространстве элементарных событий Ω, называется случайной последовательностью (случайным процессом с дискретным временем) и обозначается {Xn}, n = 1,2,... .
Замечание 2. Если последовательность состоит из детерминированных величин xn, то говорят, что последовательность сходится к величине x (это обозначается xn→ x или
| lim n→+∞ |
xn = x ), |
| {ω : |Xn(ω) - X(ω)| ≥ ε} ≠ Ж, |
Определение 2. Пусть Fn(x) и F(x) - функции распределения СВ Xn и X соответственно. Случайная последовательность {Xn}, n = 1,2,..., сходится по распределению к СВ X, если последовательность функций распределения Fn(x) СВ Xn сходится к функции распределения F(x) СВ X в каждой точке непрерывности функции F(x), т.е. Fn(x) → F(x) при n → +∞. Этот вид сходимости будем обозначать
| Xn | F → |
X. |
Пример 1. Поясним на примере случай, когда Fn(x) схоится к F(x) во всех точках за исключением конечного их числа. Пусть Xn = 1 / n, X = 0, т.е. Xn - детерминированные величины. Для них
| Fn(x) = | { | 1, x ≥ 1/n, 0, x < 1/n, |
F(x) = | { | 1, x ≥ 0, 0, x < 0. |
| Xn | F → |
X. |
Определение 3. Случайная последовательность {Xn}, n = 1,2,..., сходится почти наверное (п.н.) к СВ X, что записывается
Xn | п.н. → |
X, |
| P{ω : | lim n→+∞ |
Xn(ω) = X(ω)} = 1. |
Замечание 3. Очевидно, что если
Xn | п.н. → |
X, |
| P{ω : |
lim n→+∞ |
Xn(ω) ≠ X(ω)} = 0. |
Кроме того, легко убедиться в том, что сходимость
Xn | п.н. → |
X, |
| lim n→+∞ |
P{ | sup m≥n |
|Xm - X| ≤ ε } = 1. |
Определение 4. Случайная последовательность {Xn}, n = 1,2,..., сходится по вероятности к СВ X, что записывается как
| Xn | P → |
X. |
| lim n→+∞ |
P{|Xn - X| ≤ ε } = 1 или |
lim n→+∞ |
P{|Xn - X| > ε } = 0. |
Замечание 4. Сходимость п.н. для случайной последовательности влечет за собой и сходимость по вероятности. Действительно,
| {|Xn - X| ≥ ε } К {
| sup m≥n |
|Xm - X| ≤ ε }. |
| lim n→+∞ |
P{|Xn - X| ≤ ε } ≥ |
lim n→+∞ |
P{ | sup m≥n |
|Xm - X| ≤ ε } = 1. |
Замечание 5. Если
| Xn | P → |
X, |
| Xn | F → |
X. |
Замечание 6. В биржевом парадоксе мы имели сходимость
| Zn | P → |
0 |
Теорема 1. (неравенство Чебышева) Пусть r-й абсолютный момент СВ X конечен, т.е. M[|X|r] < +∞. Тогда для всех ε > 0 выполняется неравенство:
Доказательство. Для простоты доказательства предположим, что у СВ X существует плотность распределения fX(x). Тогда
M[|X|r] |
Δ = |
+∞ ∫ -∞ |
|x|rfX(x) dx ≥ |
∫ |x|≥ε |
|x|rfX(x) dx ≥ |
≥ εr |
∫ |x|≥ε |
fX(x) dx |
3)f(x) = |
εrP{|X| ≥ ε}, |
Замечание 7. Рассмотрим СВ
Y |
Δ = |
X - mX, где mX |
Δ = |
M[X]. |
P{|X - mX| ≥ ε} ≤ |
M[|X - mX|2] ε2 |
Δ = |
D[X] ε2 |
. |
Определение 5. Случайная последовательность {Xn}, n = 1,2,..., сходится к СВ X в среднем квадратическом, что записывается как
| Xn | с.к. → |
X, |
Замечание 8. Покажем, что если
| Xn | с.к. → |
X, |
| Xn | P → |
X. |
Yn |
Δ = |
Xn - X. |
P{|Yn| > ε} ≤ P{|Yn| ≥ ε} ≤ |
M[Yn2] ε2 |
Δ = |
M[|Xn - X|2] ε2 |
. |
| Xn | с.к. → |
X, |
| Xn | P → |
X. |
Замечание 9. Связь между различными видами сходимости удобно представить в виде логической схемы (рис.1).
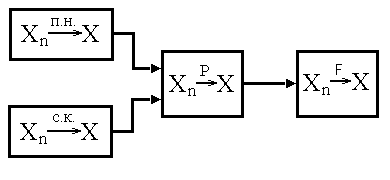
Рисунок 1.
2. Сходимость усредненной суммы случайных величин |

Определение 1. Будем говорить, что случайная последовательность {Xn}, n = 1,2,..., является последовательностью независимых СВ Xn, если при любом n СВ X1,... , Xn независимы.
Замечание 1. Рассмотрим усредненную сумму
Yn | Δ = |
1 n |
n ∑ k=1 |
Xk |
mk | Δ = |
M[Xk], k = 1,n. |
M[Yn] = |
1 n |
n ∑ k=1 |
M[Xk] |
Δ = |
1 n |
n ∑ k=1 |
mk, D[Yn] |
4)M[X] = |
1 n2 |
n ∑ k=1 |
D[Xk]. |
Определение 2. Будем говорить, что к последовательности {Xn}, n = 1,2,..., независимых СВ применим закон больших чисел, если
|Yn - M[Yn]| |
P → |
0 при n → +∞. |
Теорема 1. Если для последовательности {Xn}, n = 1,2,..., независимых СВ выполняется условие
lim n→+∞ |
D[Yn] = 0, |
Доказательство. Утверждение теоремы равносильно тому, что
lim n→+∞ |
P{|Yn - M[Yn]| > ε} = 0. |
P{|Yn - M[Yn]| > ε } ≤ P{|Yn - M[Yn]| ≥ ε} ≤ |
D[Yn] ε2 |
. |
|Yn - M[Yn]| |
P → |
0. |
Замечание 2. Утверждение теоремы верно, если СВ {Xn}, n = 1,2,..., являются лишь некоррелированными, так как свойство 4)M[X] сохраняется и для некоррелированных СВ.
Теорема 2. (Чебышев) Если у последовательности {Xn}, n = 1,2,..., независимых СВ дисперсии этих СВ равномерно ограничены, т.е. D[Xn] ≤ C для всех n = 1,2,... , то к этой последовательности применим закон больших чисел.
Доказательство. Так как D[Xn] ≤ C для всех k = 1,2,... , то
| D[Yn] | 4)M[X] = |
1 n2 |
n ∑ k=1 |
D[Xk] ≤ | C n | . |
Теорема 3. Если последовательность {Xn}, n = 1,2,..., образуют независимые СВ с одинаковыми распределениями и конечной дисперсией dX < +∞, то к этой последовательности применим закон больших чисел, причем
Yn |
P → |
mX, где mX = mk |
Δ = | M[Xk], k = 1,2,... . |
Доказательство. В данном случае D[Xk] = dX < +∞ для всех k = 1,2,... Поэтому условие теоремы Чебышева выполнено. Кроме того
M[Xk] | Δ = |
mk = mX |
| M[Yn] = | 1 n |
n ∑ k=1 |
mk = mX, |
|Yn - mX| |
P → |
0, |
Yn |
P → |
mX. |
Определение 3. Будем говорить, что к последовательности {Xn}, n = 1,2,..., независимых СВ применим усиленный закон больших чисел, если
|Yn - M[Yn]| |
п.н. → |
0 при n → +∞. |
Замечание 3. Из усиленного закона больших чисел следует просто закон больших чисел, так как по замечанию Л10.Р1.З4 из сходимости почти наверное следует сходимость по вероятности.
Теорема 4. (Колмогоров) Для последовательности {Xn}, n = 1,2,..., независимых одинаково распределенных СВ, у которых |mX| конечно, применим усиленный закон больших чисел, т.е.
Yn |
п.н. → |
mX. |
Замечание 4. В данной теореме в отличие от теоремы 3 не требуется существование дисперсии СВ Xn. Но доказательство этой теоремы значительно сложнее, чем доказательство теоремы 3.
Замечание 5. Закон больших чисел - это, по сути, свойство случайной последовательности Xn, n = 1,2,..., состоящее в том, что редкие случайные отклонения отдельных независимых СВ Xn от их общего среднего значения mX при большом n в своей массе взаимно погашаются. Поэтому, хотя сами величины Xn случайны, их среднее значение при достаточно большом n практически уже не случайно и близко к mX. Таким образом, если МО mX СВ Xn заранее неизвестно, то согласно теореме 4 его можно вычислить с любой "степенью точности" с помощью среднего арифметического
Yn |
Δ = |
1 n |
n ∑ k=1 |
Xk. |
Замечание 6. Рассмотрим бесконечную последовательность независимых испытаний (опытов) с двумя исходами (событиями) A и A, которые называются, соответственно, успехом и неуспехом, причем P(A) = p, P(A)= q = 1-p. Построенная схема испытаний называется схемой Бернулли. Рассмотрим частоту успехов
Wn |
Δ = |
M n |
, |
Теорема 5. (Бернулли) Частота успехов сходится почти наверное к вероятности события A, т.е.
Wn(A) |
п.н. → |
P(A) |
Δ = |
p. |
Доказательство. Так как M имеет биномиальное распределение, то частоту успехов Wn = M/n можно представить в виде усредненной суммы независимых одинаково распределенных СВ Xk, k = 1,n, имеющих распределение Бернулли, со значениями xk = 0 или xk = 1. Причем P{Xk = 1} = p, P{Xk = 0} = q. Поэтому
Yn = |
M n |
= |
1 n |
n ∑ k=1 |
Xk, где M[Xk] = p, D[Xk] = pq , k = 1,2,... |
M n |
п.н. → |
p. |
Замечание 7. Теорема Бернулли объясняет смысл свойства устойчивости частоты
Wn |
Δ = |
M n |
, |
