Лекция 6. Основные непрерывные распределения |
1. Равномерное распределение |

Лекция 6. Основные непрерывные распределения |
1. Равномерное распределение |

Определение 1.
СВ X распределена равномерно на отрезке [a,b], (X ~ R(а,b)), если (см. рис.1)f(x)= |
{ | 1 b - a 0 |
, , | x О [a,b], x П [a,b]. |
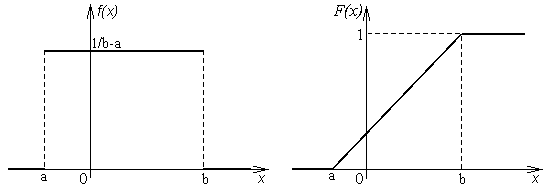
Рисунок 1 Рисунок 2.
Замечание 1. Нетрудно убедиться в том, что
функция распределения имеем вид (см. рис.2)F(x) |
Δ = |
x ∫ -∞ |
f(x) dx = |
{ |
0 x-a b-a 1 |
, x < a, , a ≤ x ≤ b, , x > b. |
Замечание 2.
Характеристическая функция СВ X ~ R(а,b):g(t) | Δ = |
M[eitx]= |
+∞ ∫ -∞ |
eitxf(x) dx = |
1 b-a |
b ∫ a |
eitx dx = |
eitb-eita it(b-a) |
. |
Замечание 3. МО и
дисперсия по определению равныmx | Δ = |
ν1 = |
+∞ ∫ -∞ |
xf(x) dx = | b ∫ a |
x b-a |
dx = | b2-a2 2(b-a) |
= | a+b 2 | , |
ν2 | Δ = |
+∞ ∫ -∞ |
x2f(x) dx = | 1 b-a |
b ∫ a |
x2 dx = | b3-a3 3(b-a) | = | b2+ba+a2 3 | , |
dx | Δ = |
μ2 |
6)mx = |
ν2 - mx2 = |
b2+ba+a2 3 | - |
a2+2ba+b2 4 | = |
(b-a)2 12 | . |
Замечание 4. Линейное преобразование
Y | Δ = |
X-a b-a |
FY(x) |
Δ = |
P{Y ≤ y} = P{X ≤ (b - a)y + a} |
Зам.1 = |
{ |
0, y, 1, |
y < 0, 0 ≤ y ≤ 1, y > 1. |
Замечание 5.
Равномерное распределение является непрерывным аналогом дискретного распределения вероятностей для опытов с равновероятными исходами.Замечание 6. Погрешность приближенных вычислений каких-либо параметров при округлении до ближайших целых чисел удовлетворительно описывается
распределением R(-1/2, 1/2).Замечание 7. Если СВ Y имеет непрерывную строго возрастающую
функцию распределения FY(y), то можно показать, что СВX |
Δ = |
FY(Y) |
Fx(x) |
Δ = |
P{FY(Y) ≤ x} = P{Y ≤ FY-1(x)} = FY(FY-1(x)) = x. |
Y |
Δ = |
FY-1(X) |
2. Экспоненциальное распределение |

Определение 1.
СВ X имеет экспоненциальное (показательное) распределение с параметром λ > 0 (X ~ E(λ)), если (см. рис.3)f(x)= |
{ | λe-λx 0 |
, , | если x ≥ 0, если x < 0. |
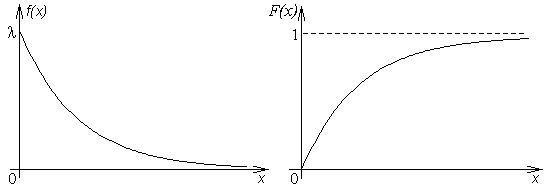
Рисунок 3 Рисунок 4.
Замечание 1.
Функция распределения СВ X ~ E(λ) равна (см. рис.4): F(x) = 0, если x < 0, иF(x) |
Δ = |
x ∫ -∞ |
f(x) dx = | f(x) = 0 ,если x < 0 | = λ |
x ∫ 0 |
e-λx dx = 1 - e-λx, x ≥ 0. |
Замечание 2.
Характеристическая функция СВ X ~ Е(λ):g(t) | Δ = |
+∞ ∫ -∞ |
eitxf(x) dx = λ |
+∞ ∫ 0 |
e-λxeitx dx = λ |
+∞ ∫ 0 |
ex(it-λ) dx = |
| = | λ it-λ |
ex(it-λ) | | | +∞ x=0 |
= | λ λ-it |
. |
Замечание 3.
Найдём МО и дисперсию СВ X ~ E(λ):mx |
Δ = |
ν1 = |
1 i |
d dt |
g(t) |
| | t =0 |
= |
λ (λ-it)2 |
| | t =0 |
= | 1 λ |
, |
ν2 = |
1 i2 |
d2 dt2 |
g(t) |
| | t =0 | = |
2λ (λ-it)3 |
| | t =0 |
= | 2 λ2 |
, |
dx |
6)mx = |
ν2 - ν12 = |
1 λ2 |
. |
Замечание 4.
Экспоненциальное распределение является одним из основных распределений, используемых в теории надежности. Например, продолжительность безотказной работы многих технических устройств, а также время задержки вылета самолёта по вине технических служб аэропорта удовлетворительно описываются соответствующими экспоненциальными распределениями.3. Нормальное распределение |

Определение 1.
СВ X имеет нормальное (гауссовское) распределение с параметрами m и σ > 0 (X ~ N(m,s)), если (см. рис.5)| f(x) = | 1 √2πσ | exp | { | - | (x-m)2 2σ2 |
} | . |
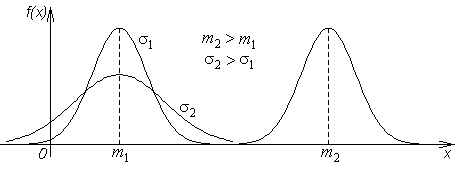
Рисунок 5.
Замечание 1.
Графики плотности нормального распределения, называемые кривыми Гаусса, имеют единственный максимум в точке x = m. Найдём функцию распределения СВ X ~ N(m,σ):F(x) |
Δ = |
x ∫ -∞ |
f(x) dx = |
1 σ√2π | x ∫ -∞ |
exp | { | - |
(x-m)2 2σ2 |
} | dx = |
= | | | y | Δ = |
x-m σ | , |
dy = | 1 σ |
dx | | | = |
= |
1 √2π | (x-m)/ σ ∫ -∞ |
e-y | 2 | /2 dy = Φ |
[ | x-m σ |
] | . |
Φ(y) |
Δ = |
1 √2π | y ∫ -∞ |
e-y | 2 | /2 dy |
Φ0(y) |
Δ = |
1 √2π | y ∫ 0 |
e-x | 2 | /2 dx , |
при y > 0. |
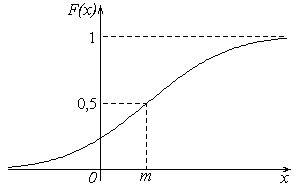
Рисунок 6.
Замечание 2.
Характеристическая функция СВ X ~ N(0,1) имеет видg(t)= e-t | 2 | /2. |
g(t) = |
1 √2π | +∞ ∫ -∞ |
e-x | 2 | /2eitx dx = |
| | формула Эйлера |
| | = |
= | 1 √2π | +∞ ∫ -∞ |
e-x | 2 | /2cos tx dx + |
i √2π | +∞ ∫ -∞ |
e-x | 2 | /2sin tx dx = |
= | | |
sin tx - нечетная , |
e-x | 2 | /2 - четная , пределы симметр. |
| | = |
= | 1 √2π | +∞ ∫ -∞ |
e-x | 2 | /2cos tx dx ; |
g'(t) = - |
1 √2π | +∞ ∫ -∞ |
xe-x | 2 | /2sin tx dx = |
| | интегрирование по частям |
| | = |
= |
1 √2π | [ |
e-x | 2 | /2sin tx |
| | +∞ -∞ |
- |
+∞ ∫ -∞ |
e-x | 2 | /2cos tx dx |
] | = -t g(t), |
* X | Δ = |
X-m σ |
g(t)= e-t | 2 | /2. |
X | Δ = σ |
* X | + m |
gx(t) = eitmg |
* X |
(σt) = exp(itm - t2 σ 2 / 2) . |
Замечание 3.
МО и дисперсия СВ X ~ N(m,σ) равныν1 = |
1 i |
d dt |
g(t) |
| | t =0 |
= |
(im-tσ2) i |
= exp(imt - t2σ2/2) |
| | t =0 |
= m, |
ν2 = |
1 i2 |
d2 dt2 |
g(t) |
| | t =0 | = |
1 i2 |
[ |
- σ2exp(imt - t2σ2/2) + |
+ (im - tσ2)2exp(imt - t2σ2/2) |
] | t =0 | = - |
σ2+m2 i2 | = σ2+m2 , |
dx |
6)mx = |
ν2 - ν12 = σ2. |
Замечание 4. С помощью линейного преобразования
* X | Δ = |
X-m σ |
F | * X |
(x) = Φ(x). |
Замечание 5.
Нормально распределенная СВ с большой вероятностью принимает значения, близкие к своему МО, что называют "правилом k сигм":P{|X - m| ≤ kσ} | З1 = |
Φ(k) - Φ(-k) = |
{ |
0.6827 , k = 1, 0.9545 , k = 2, 0.9973 , k = 3. |
Замечание 6.
Нормальное распределение имеет очень широкое распространение в прикладных задачах. Это связано с тем, что в реальной жизни многие исследуемые СВ являются следствием разлияных случайных событий. В частности, при достаточно общих предположениях сумма большого числа независимых СВ имеет распределение близкое к нормальному (точные формулировки см. ниже, Теорема Л11.Р1.Т2).Пример 1. Рост людей на нашей планете хорошо описывается нормальным распределением. Это, по-видимому, связано с тем, что на рост влияют разнообразные независимые случайные факторы: климат, экология окружающей среды, экономические условия, болезни и т.д. Хотя, конечно, "бесконечно" большие люди (великаны) и "бесконечно" маленькие люди (гномы) бывают только в сказках. Это говорит о том, что "хвосты" истинного распределения роста людей отличаются от нормального распределения.
4. Распределение Вейбулла |

Определение 1.
СВ X имеет распределение Вейбулла с параметрами α и λ, λ > 0, α > 0, если (см. рис.7)fx(x)= | { |
αλxα-1e-λx |
α | , x ≥ 0, |
| 0 | , x < 0. |
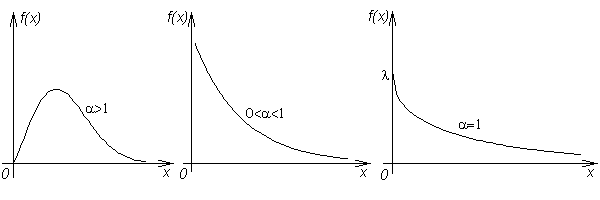
Рисунок 7.
Замечание 1. Нетрудно убедиться, что
Fx(x) |
Δ = |
x ∫ -∞ |
fx(t) dt = |
{ | 1 - e-λx |
α | , x ≥ 0, |
| 0 |
, x < 0. |
Замечание 2. Приведем вид МО и
дисперсии| mx = λ-1/α Γ | [ | α+1 α |
] | , |
| dx = λ-2/α | { | 2 α |
Γ | [ | 2 α |
] | - | 2 α2 |
[ | Γ | ( | 1 α | ) | ] | 2 |
} | , |
Γ(x) | Δ = |
+∞ ∫ 0 |
e-t tx-1 dt - |
Замечание 3. Если α = 1, то
распределение Вейбулла превращается в показательное распределение.Замечание 4.
СВ, имеющая распределение Вейбулла, встречается в задачах надежности при оценке времени безотказной работы прибора .5. Логарифмически нормальное распределение |

Определение 1.
СВY | Δ = |
ex, |
Замечание 1. Так как ex - строго возрастающая функция, то, учитывая вид нормального распределения (определение
Л6.Р1.О1), найдём плотность логнормального распределенияfY(y) | 4)f(x) = |
fx(ψ(y))ψ'(y) = |
| | ψ(y) = ln y ψ'(y) = 1/y |
| | = |
= |
{ |
|
, y > 0, y ≤ 0. |
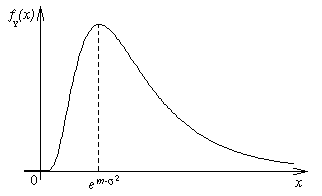
Рисунок 8.
Замечание 2. Найдём МО и дисперсию СВ Y. По определению:
M[Y] = |
1 σ√2π | +∞ ∫ 0 |
exp{-(ln y - m)2/2σ2} dy = |
| | замена перем. y = exp{σ(t + σ) + m} |
| | = |
= | exp{m + σ2/2} √2π | +∞ ∫ -∞ |
e-t |
2 | /2 dt = exp{m + σ2/2}. |
Замечание 3. Логнормальное распределение широко используется в экономической статистике, статистической физике и др.
