Типовая задача 8.2

Задача 1.   Для случайной величины ξ ~ R(0,4) вычислить

Pk = P{|ξ - M[ξ]| < k√D[ξ]}
при k = 1, 2, 3.

Решение.   Плотность вероятности f(x) случайной величины ξ ~ R(0,4) такова:

f'(x) =		 { 1
4
0,
, если 0 < x < 4,

  в остальных случаях.
Её график представлен на рисунке 1:

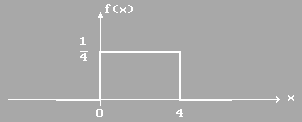
Рисунок 1
Рисунок 1

Учитывая, что
M[ξ] = 4+0
  2		 = 2, D[ξ] = (4-0)2
  12		 = 4
3		 ,
перепишем искомую вероятность в виде
Pk = P{|ξ - 2| < 2k
√3		 } = P{2 - 2k
√3		 < ξ < 2+ 2k
√3		 }.
Таким образом,
P1 = P{2 -  2
√3		 < ξ < 2 +  2
√3		 } = 2+2/√3
  ∫
2-2/√3		 f(x) dx = 2+2/√3
  ∫
2-2/√3		 1
4		 dx =  1
√3		 .
Далее,
P2 = P{2 -  4
√3		 < ξ < 2 +  4
√3		 } = 2+4/√3
  ∫
2-4/√3		 f(x) dx .
Как легко видеть,
2 -  4
√3		 < 0,   2 +  4
√3		 > 4.
Поэтому при дальнейшем вычислении P2 под знаком полученного интеграла нельзя формально f(x) заменить на 1 / 4, ведь f(x) = 1 / 4 не для всех значений x, а лишь для 0 < x < 4. Очевидно, что
P2 = 2+4/√3
  ∫
2-4/√3		 f(x) dx = 4
∫
0		 1
4		 dx = 1.
(Иначе можно было бы сказать так:
2 -  4
√3		 < ξ < 2 +  4
√3		 - достоверное событие.)
Вероятность P3 = P{|ξ - M[ξ]| < 3√D[ξ]} не меньше вероятности P2, то есть P3 ≥ 1. Но P3 > 1 невозможно. Следовательно, P3 = 1.


Выход в меню занятия

Hosted by uCoz