Занятие №8: Типовая задача 8.1

Типовая задача 8.1

Задача 1. В круге радиуса r с центром в точке O наугад выбирается точка M (см. рис.1). Найти функцию распределения, плотность вероятности, математическое ожидание и дисперсию случайной величины ξ, равной расстоянию между точками O и M.

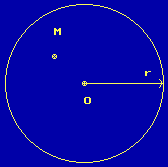
Рисунок 1

Решение. Прежде всего уточним условие задачи. Говоря о случайном выборе точки M в данном круге, мы подразумеваем, что вероятность оказаться точке M в произвольной (квадратируемой) части этого круга равна отношению площади этой части круга к площади всего круга. Поэтому при 0 < x < r (см. рис.2)

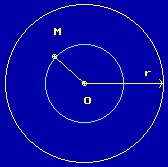
Рисунок 2

P{ξ ≤ x} =

Очевидно также, что при x < 0 P{ξ ≤ x} = 0, а при x > r P{ξ ≤ x} = 1. Таким образом,

если x < 0,

, если 0 ≤ x ≤ r,

если x > r.

График построенной функции F(x) представлен на рис. 3

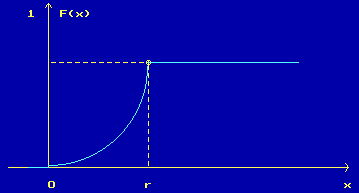
Рисунок 3

Во всех точках числовой прямой, кроме точки x = r, функция F(x) дифференцируема. При этом

если x < 0 или x > r,

, если 0 ≤ x ≤ r.

Доопределяя функцию F'(x) в точке x = r (например, как значение выражения 2x / r² при x = r) получим функцию

если x < 0 или x > r,

, если 0 ≤ x ≤ r,

которую можно рассматривать как плотность вероятности случайной величины ξ. График функции f(x) показан на рис. 4.

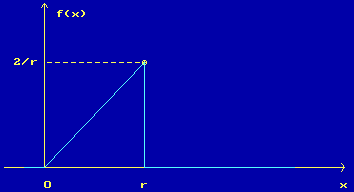
Рисунок 4

Далее, получаем

D[ξ] = M[ξ²] - (M[ξ])² =

Выход в меню занятия