Занятие №7: Типовая задача 7.2

Типовая задача 7.2

Задача 1. Известно, что ξ имеет распределение Bi(n,p), причём M[ξ] = 1, D[ξ] = 0,96. Найдите наиболее вероятное значение случайной величины ξ.

Решение. На рис.1-4 представлены типовые случаи изменения вероятности

P_n(m) = P{ξ = m} = C_n^mp^mq^n-m

при изменении m. Всегда можно указать одно (рис.1,3,4) или два (рис.2) значения величины ξ, которые имеют наибольшую вероятность.

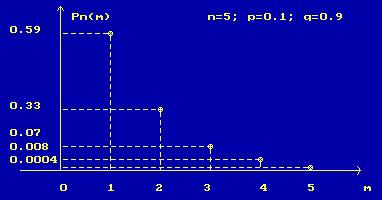
Рисунок 1

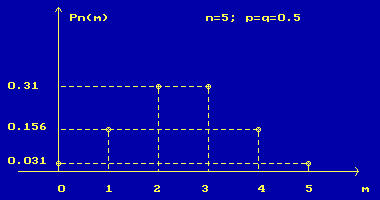
Рисунок 2

Рисунок 3

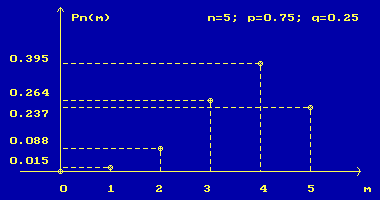
Рисунок 4

Обозначим m₀ - значение величины ξ, которому соответствует наибольшая вероятность. Можно доказать, что

m₀=

{

[np - q] + 1, если np - q - нецелое число,
np - q и np-q + 1, если np - q - целое число,

где символом [.] обозначена целая часть числа. Этим мы и воспользуемся при решении данной задачи (а также некоторых из приводимых ниже задач). По условию задачи np = 1, npq = 0,96. Следовательно, q = 0,96, p = 0,04, n = 25. Число np - q = 1 - 0,96 = 0,04 - дробное. Поэтому данная величина ξ имеет единственное наиболее вероятное значение m₀ = [np - q] + 1 = [0,04] + 1 = 0 + 1 = 1.

Типовая задача 7.2

Выход в меню занятия