Типовая задача 7.1

Задача 1.   Случайная величина ξ принимает значения -2, -1, 0, 1, 2. Вероятности первых четырех значений приведены в следующей таблице:
ξ-2-1012
p0,10,30,20,2 
Построить график функции распределения величины ξ. Найти математическое ожидание и дисперсию величины ξ, а также вероятность

P{|ξ - M[ξ]| ≤ √D[ξ]}.

Решение.   Неизвестная вероятность P{ξ = 2} находится из условия, что сумма вероятностей всех значений величины ξ равна 1:

0,1 + 0,3 + 0,2 + 0,2 + P{ξ=2} = 1.
Отыскав эту вероятность, P{ξ=2} = 0,2, построим график функции распределения F(x) случайной величины ξ. Он представляет собой ступенчатую (кусочно-постоянную) функцию со скачками в точках -2, -1, 0, 1, 2, равными соответствующим вероятностям: 0,1; 0,3; 0,2; 0,2; 0,2 (рис.1).

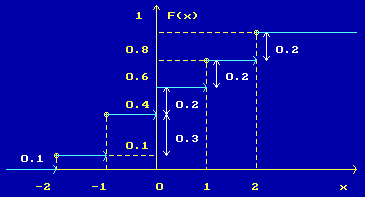
Рисунок 1
Рисунок 1

Стрелочки на рисунке поставлены для различения значений функции F(x) в точках разрыва. Следует запомнить, что функция распределения F(x) всякой (а не только дискретной) случайной величины ξ непрерывна справа. Математическое ожидание M[ξ] найдем, сложив произведения значений величины ξ на их вероятности:
M[ξ] = (-2)•0,1 + (-1)•0,3 + 0•0,2 + 1•0,2 + 2•0,2 = 0,1.
Для вычисления D[ξ] используем формулу
D[ξ] = M[ξ2] - (M[ξ])2 ,
предварительно отыскав M[ξ2]. Имеем:
M[ξ2] = (-2)2•0,1 + (-1)2•0,3 + 02•0,2 + 12•0,2 + 22•0,2 = 1,7;
Далее получаем:
P{|ξ - M[ξ]| ≤ √D[ξ]} = P{|ξ - 0,1| ≤ √1,69} =
= P{|ξ - 0,1| ≤ 1,3} = P{ -1,3 ≤ ξ-0,1 ≤ 1,3 } = P{ -1,2 ≤ ξ-0,1 ≤ 1,4 }.
Событие { -1,2 ≤ ξ-0,1 ≤ 1,4 } наблюдается тогда и только тогда, когда ξ принимает одно из значений: -1, 0, 1. Таким образом,
P{|ξ - M[ξ]| ≤ √D[ξ]} = P{ξ = -1} + P{ξ = 0} + P{ξ = 1} = 0,3 + 0,2 + 0,2 = 0,7.



Выход в меню занятия

Hosted by uCoz