Типовая задача 11.2 |

Типовая задача 11.2 |

Задача 1. Известно, что X и Y независимые СВ, и каждая из них распределена равномерно на интервале (0,1). Найти закон распределения их суммы Z = X + Y.
Решение. Пусть fX(x), fY(Y) и fZ(z) - плотности вероятности случайных величин X, Y и Z соответственно. Тогда, как известно,
| fZ(z) = | +∞ ∫ -∞ |
fX(x)fY(z - x) dx. |
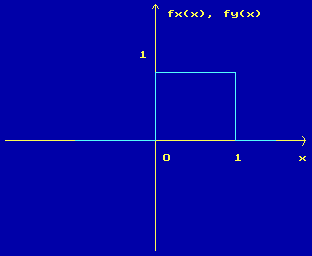
Рисунок 1
| fZ(z) = | ∫ x : 0≤x≤1 0≤z - x≤1 |
dx = | ∫ x : 0≤x≤1 0≤z - x≤1 |
dx = | min(1,z) ∫ max(0,z-1) |
dx = min(1,z) - max(0,z-1) = |
| = | { | z, 2-z, 0 |
если 0 ≤ z ≤ 1 ; если 1 ≤ z ≤ 2 ; в остальных случаях . |
