Контрольные задачи 8.3 |

Контрольные задачи 8.3 |

Задача 1. Какое событие для случайной величины ξ ~ E(λ) более вероятно: а) ξ > M[ξ] или ξ < M[ξ]; б) ξ > M[ξ] или ξ > √D[ξ]?
Задача 2. На одном чертеже приведите графики плотностей вероятностей f1(x) и f2(x) величин ξ ~ E(2), а на другом чертеже - графики соответствующих функций распределения F1(x) и F2(x).

Рисунок 1
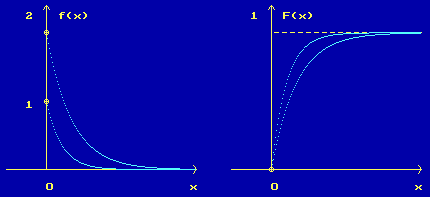
Рисунок 2
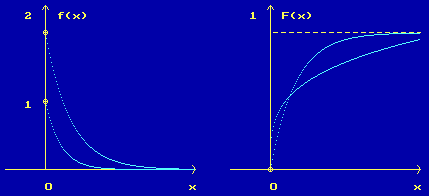
Рисунок 3
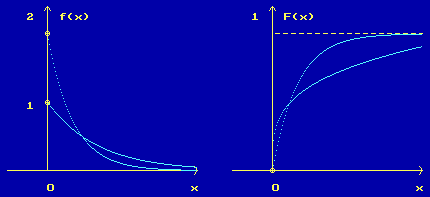
Рисунок 4
Задача 3. Докажите, что для СВ ξ ~ E(λ)